Top posters
| zelel (582) | ||||
| †MrKut3o† (313) | ||||
| [chún_ạk] (296) | ||||
| __!*y'- legend*!__ (267) | ||||
| december.28 (255) | ||||
| •ķåηðγ• (236) | ||||
| GPS|Genji (206) | ||||
| Admin (188) | ||||
| PCD.=(¯`·.¸ C^_^D ¸.·´¯)M (182) | ||||
| billy (146) |
Latest topics
Nhị Thức NIUTON
2 posters
Diễn Đàn A1 :: Học hành :: Ban tự nhiên
Trang 1 trong tổng số 1 trang
 Nhị Thức NIUTON
Nhị Thức NIUTON
ÁP DỤNG NHỊ THỨC NEWTON ĐỂ CHỨNG MINH HỆ THỨC VÀ TÍNH TỔNG TỔ HỢP.
I. ÁP DỤNG NHỊ THỨC NEWTON ĐỂ CHỨNG MINH HỆ THứC VÀ TÍNH TỔNG TỔ HỢP.
Nguyễn Văn Năm - Lê Hoàng Nam
I. Thuần nhị thức Newton
Dấu hiệu nhận biết: Khi các số hạng của tổng đó có dạngthì ta sẽ dùng trực tiếp nhị thức Newton:
. Việc còn lại chỉ là khéo léo chọn a,b
Ví dụ 1.1: Tính tổng
Dễ dàng thấy tổng trên có dạng như dấu hiệu nêu trên. Ta sẽ chọn. Khi đó tổng trên sẽ bằng
Ví dụ 1.2: Chứng minh rằng:
Tương tự như trên, ta nghĩ ngay đến việc dùng nhị thức với:
Nhưng tổng cần tìm chỉ chứa các số hạng cóvới k chẵn nên ta phải triệt tiêu được các số hạng “lẻ”
bằng cách tính tổng khác với
Do đó tổng cần tìm là
Bài tập tương tự:
1. Chứng minh rằng:
2. Chứng minh rằng:
II. Sử dụng đạo hàm cấp 1,2
1. Đạo hàm cấp 1
Dấu hiệu: Khi hệ số đứng trước tổ hợp tăng dần hoặc giảm dần từhay
tức số hạng đó có dạng
hoặc
thì ta có thể dùng đạo hàm cấp 1 đến tính.
Cụ thể
Lấy đạo hàm hai vế theo x ta được :
(1)
Đến đây thay x,a bằng hằng số thích hợp ta được tổng cần tìm
Ví dụ II.1: Tính tổng
Giải
Ta thấy tổng cần tính có dạng như VP (1). Việc còn lại chỉ cần chọnta tính được tổng bằng 0.
Cách khác: Sử dụng đẳng thứcta được tổng bằng :
Dùng cách này có thể tránh được dùng đạo hàm do đó phù hợp với các bạn
11 chưa học đến đạo hàm hoặc cảm thấy dùng chưa quen đạo hàm.
Ví dụ II.2: Tính tổng
Giải
Nhận thấy hệ số đứng trước tổ hợp giảm dầnnên phải hoán đổi vị trí
và
:
Đạo hàm theo x:
Thay x = 2, a = 3 ta được tổng bằng
Cách khác: Khéo léo sử dụng 2 đẳng thứcta có thể tránh việc phải dùng đạo hàm phức tạm:
Ví dụ II.3: Tính tổng
Giải
Hệ số trước tổ hợp giảm dần từ 2008,2007,…2,1 nên dùng đạo hàm là điều
dễ hiểu:
Bây giờ nếu lấy đạo hàm thì chỉ đượctrong khi trong đề đến 2008 do đó ta phải nhân
thêm x vào đẳng thức trên rồi mới đạo hàm:
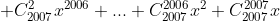
Thay x = 1 vào ta tìm được tổng là
Bài tập tương tự
1. Chứng minh rằng
2. Tính tổng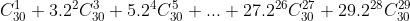
3. Tìm n biết
2. Đạo hàm cấp 2
Dấu hiệu: Khi hệ số đứng trước tổ hợp có dạnghay
hay
( không kể dấu ) tức có dạng
hay tổng quát hơn
thì ta có thể dùng đạo hàm đến cấp 2 để tính. Xét
đa thức:
Khi đó đạo hàm hai vế theo x ta được:
Đạo hàm lần nữa:
Đến đây ta gần như giải quyết xong bài toán chỉ việc thay a, b, x bởi
các hằng số thích hợp nữa thôi.
Ví dụ II.4: Chứng minh rằng
S =
Dễ dàng thấy được VT của đẳng thức trên giống gần như hoàn toàn VP (2)
ta chỉ việc thay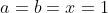
là đã giải quyết xong bài toán
Chú ý: Đây chỉ là ý tưởng còn khi trình bày vào bài kiểm
tra hay bài thi thì ta phải ghi rõ xét đa thứcrồi đạo hàm 2 lần và thay x = 1 vào mới được trọn
số điểm.
Cách khác: Ta vẫn có thể sử dụng được đẳng thức2 lần để tính tổng trên, cụ thể:
Tương tự như trên ta dễ dàng tính được tổng bằng cách thay x = -1 và n =
16
Hoặc ta cũng có thể sử dụngđể đơn giản hơn một chút.
Ví dụ II.5: Rút gọn tổng sau
Giải
Với ý tưởng như bài trên ta xét đa thức
Đạo hàm lần 1:
Nếu ta tiếp tục đạo hàm lần nữa thì chỉ thu được 1.2, 2.3 ,… do đó để
thu đượcta phải nhân thêm hai vế với x rồi mới lấy đạo
hàm:
Thay x = 1 ta rút gọn được tổng trên thành
Tương tự khi tính tổngta cần chú ý là trước tổ hợp có một hệ số lớn
hơn k trongnên ta phải nhân với x trước khi đạo hàm 2 lần.
Bài tập tương tự:
1. Tính tổng
Được sửa bởi __!*y'- legend*!__ ngày Sun May 16, 2010 7:24 pm; sửa lần 1.

__!*y'- legend*!__- To mồm

- Tổng số bài gửi : 267
Phiếu bé ngoan : 675
Số lần được cám ơn : -4
Join date : 13/04/2009
Age : 32
Đến từ : hà nội 1
 Re: Nhị Thức NIUTON
Re: Nhị Thức NIUTON
III. Sử dụng tích phân xác định
Dấu hiệu: Ý tưởng của phương pháp này là dựa vào hệ thức
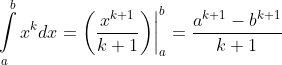
Từ đấy dễ dàng tìm được dấu hiệu để sử dụng phương pháp này là số hạng
của tổng có dạng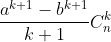 . Cụ thể, xét tích phân
. Cụ thể, xét tích phân 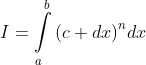 ta có thể tính bằng hai cách.
ta có thể tính bằng hai cách.
Tính trực tiếp: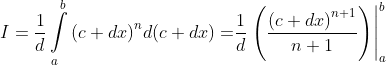
Hoặc gián tiếp:
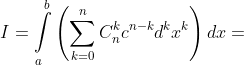
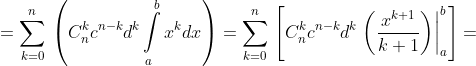
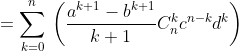
Hai cách trên là như nhau nên từ đó ta có được:

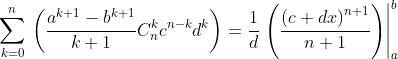
Tùy bài toán ta chọn các hệ số a, b, c, d, thích hợp
Ví dụ III.1: CMR
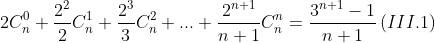
Giải
Nhìn vào tử của phân số dễ dàng tìm được hai cận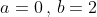 .
.
Tiếp tục để ý một chút ta chọn tiếp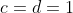 suy
suy
ra đpcm
Chú ý: Khi trình bày bài thi phải ghi rõ tích phân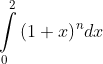
rồi tính bằng hai cách mới được trọn điểm.
Cách khác: Ta có thể tránh không dùng tích phân bằng cách
áp dụng đẳng thức: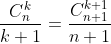 . Việc tính toán không những đơn giản hơn mà còn
. Việc tính toán không những đơn giản hơn mà còn
giảm thiểu được sai sót khi làm bài:
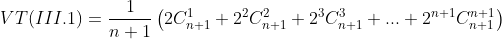
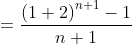
Để thấy rõ sự hữu ích của đẳng thức đơn giản đó, ta xét một ví dụ khác.
Tính tổng

Rõ ràng dùng tích phân đối với bài này gần như là không thể nhưng nếu
áp dụng đẳng thức đó thì lại là một chuyện khác:
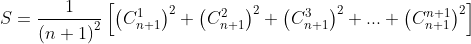
Việc còn lại bây giờ chỉ là tính tổng trong ngoặc vuông đó. Có rất
nhiều cách để tính nên chúng ta sẽ quay lại tổng này trong phần “ Các
phương pháp khác “.
Trở lại phần tích phân, với việc thay a, b, c, d bằng cách hằng số
thích hợp ta có thể “chể” ra các bài toán phức tạp hơn, chẳng hạn khi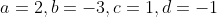 ta có:
ta có:
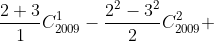
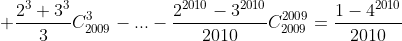
Ví dụ III.2: Tính
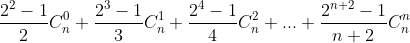
Giải
Mỗi số hạng của tổng có dạng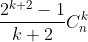 nên ta nghĩ ngay đến dùng tích phân. Nhưng mẫu
nên ta nghĩ ngay đến dùng tích phân. Nhưng mẫu
của hệ số lại là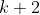 so với
so với
trong dấu hiệu ở trên là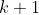 . Do
. Do
đó ta phải thay tích phân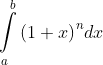 bằng tích phân khác. Ở đây ta chọn
bằng tích phân khác. Ở đây ta chọn 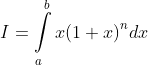 .
.
Dễ dàng tìm được cận trên là 2, cận dưới là 1. Thử lại:
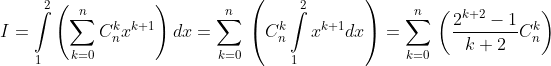
Việc còn lại bây giờ chỉ là đi tính trực tiếp I:
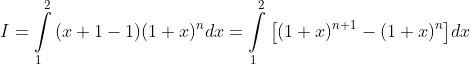
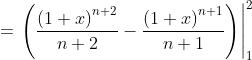
Với ý tưởng đó ta xét tổng sau:
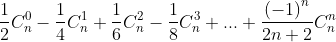
Mẫu của hệ số trước tổ hợp giờ đây không còn mẫu mực nữa mà “nhảy cóc”
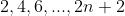
và để ý mỗi số hạng có dạng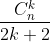 nên số hạng ban đầu của nó trước khi lấy nguyên
nên số hạng ban đầu của nó trước khi lấy nguyên
hàm là hay
hay 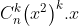 đến đây phần nào ta đã đoán ra được tích phân ban
đến đây phần nào ta đã đoán ra được tích phân ban
đầu là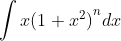 . Nhưng như vậy thì dấu trừ ở đâu ra ?
. Nhưng như vậy thì dấu trừ ở đâu ra ?
Tinh ý một chút ta sửa lại được: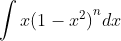 . Việc thay cận đơn giản hơn, ở đây ta chọn cận
. Việc thay cận đơn giản hơn, ở đây ta chọn cận
trên là 1, cận dưới là 0. Thử lại tí chút:
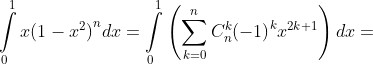
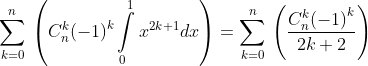
Phần còn lại của bài toán là tính tích phân đó:
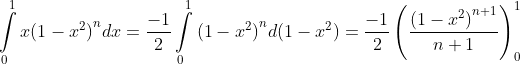
Với việc thay đổi tích phân ta có thể làm ra ti tỉ các tổng khác phức
tạp hơn ^^!. Ví dụ
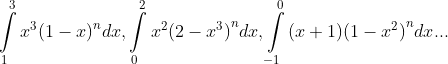
Một số bài tương tự:
1. Tính tổng bằng hai cách:
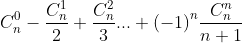
( HD: tương tự ví dụ III.1 )
2. Tính tổng bằng hai cách:
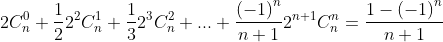
( HD: tương tự ví dụ III.1 )
3. Chứng minh rằng
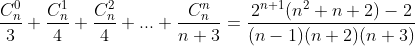
( HD: tương tự ví dụ III.2 )
4. Chứng minh rằng
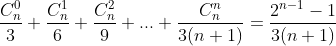
Dấu hiệu: Ý tưởng của phương pháp này là dựa vào hệ thức
Từ đấy dễ dàng tìm được dấu hiệu để sử dụng phương pháp này là số hạng
của tổng có dạng
Tính trực tiếp:
Hoặc gián tiếp:
Hai cách trên là như nhau nên từ đó ta có được:
Tùy bài toán ta chọn các hệ số a, b, c, d, thích hợp
Ví dụ III.1: CMR
Giải
Nhìn vào tử của phân số dễ dàng tìm được hai cận
Tiếp tục để ý một chút ta chọn tiếp
ra đpcm
Chú ý: Khi trình bày bài thi phải ghi rõ tích phân
rồi tính bằng hai cách mới được trọn điểm.
Cách khác: Ta có thể tránh không dùng tích phân bằng cách
áp dụng đẳng thức:
giảm thiểu được sai sót khi làm bài:
Để thấy rõ sự hữu ích của đẳng thức đơn giản đó, ta xét một ví dụ khác.
Tính tổng
Rõ ràng dùng tích phân đối với bài này gần như là không thể nhưng nếu
áp dụng đẳng thức đó thì lại là một chuyện khác:
Việc còn lại bây giờ chỉ là tính tổng trong ngoặc vuông đó. Có rất
nhiều cách để tính nên chúng ta sẽ quay lại tổng này trong phần “ Các
phương pháp khác “.
Trở lại phần tích phân, với việc thay a, b, c, d bằng cách hằng số
thích hợp ta có thể “chể” ra các bài toán phức tạp hơn, chẳng hạn khi
Ví dụ III.2: Tính
Giải
Mỗi số hạng của tổng có dạng
của hệ số lại là
trong dấu hiệu ở trên là
đó ta phải thay tích phân
Dễ dàng tìm được cận trên là 2, cận dưới là 1. Thử lại:
Việc còn lại bây giờ chỉ là đi tính trực tiếp I:
Với ý tưởng đó ta xét tổng sau:
Mẫu của hệ số trước tổ hợp giờ đây không còn mẫu mực nữa mà “nhảy cóc”
và để ý mỗi số hạng có dạng
hàm là
đầu là
Tinh ý một chút ta sửa lại được:
trên là 1, cận dưới là 0. Thử lại tí chút:
Phần còn lại của bài toán là tính tích phân đó:
Với việc thay đổi tích phân ta có thể làm ra ti tỉ các tổng khác phức
tạp hơn ^^!. Ví dụ
Một số bài tương tự:
1. Tính tổng bằng hai cách:
( HD: tương tự ví dụ III.1 )
2. Tính tổng bằng hai cách:
( HD: tương tự ví dụ III.1 )
3. Chứng minh rằng
( HD: tương tự ví dụ III.2 )
4. Chứng minh rằng

__!*y'- legend*!__- To mồm

- Tổng số bài gửi : 267
Phiếu bé ngoan : 675
Số lần được cám ơn : -4
Join date : 13/04/2009
Age : 32
Đến từ : hà nội 1
 Re: Nhị Thức NIUTON
Re: Nhị Thức NIUTON
V. Công cụ số phức
Ý tưởng của phương pháp này là dựa tính chất đặc biệt của i:
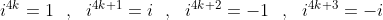 với
với 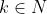
Từ đó, ta xét đa thức
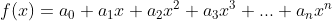
Đặt . Ta có:
. Ta có:
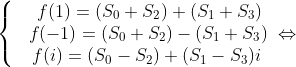
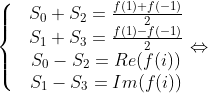
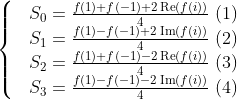
Với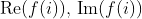 lần lượt là phần thực và phần ảo của
lần lượt là phần thực và phần ảo của 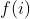 .
.
Ví dụ IV.1: Rút gọn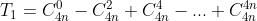 .
.
Giải
Rõ ràng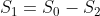 trong đa thức
trong đa thức 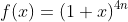 . Mặt khác ta có
. Mặt khác ta có 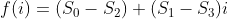 nên công việc bây giờ chỉ là đi tính
nên công việc bây giờ chỉ là đi tính 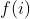
và phần thực của nó chính là tổng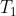 cần tìm:
cần tìm: 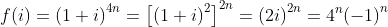 .
.
Ta cũng có thể sử dụng (1), (3) ta đã tìm ra ở trên để giải nhưng mất
công giải lại hệ phương trình 4 ẩn đó và như thế thì thật là giết ruồi
mà lại dùng đến dao mổ trâu ^^!
Tương tự ta tính được tổng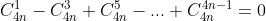
Ví dụ IV.2: Tính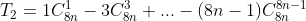
Giải
Trước tiên ta phải dùng đạo hàm để có được hệ số đứng trước tổ hợp. Xét
đa thức:
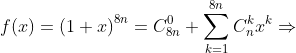

Lại nhân với x ta được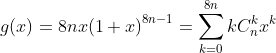
Nhận thấy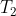 chính là phần ảo của
chính là phần ảo của  :
: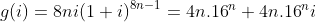
Do đó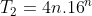
Tương tự ta dùng đạo hàm 2 lần để tính tổng:
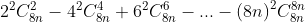 :
:
Giải:
Ta có:
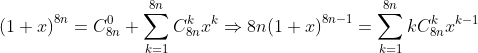
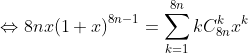

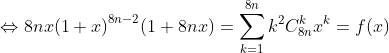
Tổng cần tính là phần thực của: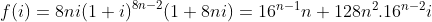
Bài tập tương tự:
Cho khai triển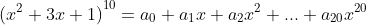 . Tính tổng
. Tính tổng
a.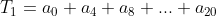 b.
b. 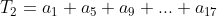
c.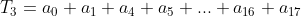 d.
d. 
Ý tưởng của phương pháp này là dựa tính chất đặc biệt của i:
Từ đó, ta xét đa thức
Đặt
Với
Ví dụ IV.1: Rút gọn
Giải
Rõ ràng
và phần thực của nó chính là tổng
Ta cũng có thể sử dụng (1), (3) ta đã tìm ra ở trên để giải nhưng mất
công giải lại hệ phương trình 4 ẩn đó và như thế thì thật là giết ruồi
mà lại dùng đến dao mổ trâu ^^!
Tương tự ta tính được tổng
Ví dụ IV.2: Tính
Giải
Trước tiên ta phải dùng đạo hàm để có được hệ số đứng trước tổ hợp. Xét
đa thức:
Lại nhân với x ta được
Nhận thấy
Do đó
Tương tự ta dùng đạo hàm 2 lần để tính tổng:
Giải:
Ta có:
Tổng cần tính là phần thực của:
Bài tập tương tự:
Cho khai triển
a.
c.

__!*y'- legend*!__- To mồm

- Tổng số bài gửi : 267
Phiếu bé ngoan : 675
Số lần được cám ơn : -4
Join date : 13/04/2009
Age : 32
Đến từ : hà nội 1
 Re: Nhị Thức NIUTON
Re: Nhị Thức NIUTON
Xin cảm ơn, rất hữu ích :x

zelel- Chiến sĩ anh hùng

- Tổng số bài gửi : 582
Phiếu bé ngoan : 219788
Số lần được cám ơn : 44
Join date : 10/04/2009
Age : 32
Đến từ : Chuồng vịt siêu thịt
Bản thân
IQ: Là cái j`???
Độ ưa nhìn:


 (0/10)
(0/10)
 Re: Nhị Thức NIUTON
Re: Nhị Thức NIUTON
qua ngon con j.. :))

__!*y'- legend*!__- To mồm

- Tổng số bài gửi : 267
Phiếu bé ngoan : 675
Số lần được cám ơn : -4
Join date : 13/04/2009
Age : 32
Đến từ : hà nội 1
Diễn Đàn A1 :: Học hành :: Ban tự nhiên
Trang 1 trong tổng số 1 trang
Permissions in this forum:
Bạn không có quyền trả lời bài viết
» Học tiếng Nhật - Top Globis
» Học tiếng Nhật - Top Globis
» Tiếng Nhật online xu thế mới của thời đại- Top Globis
» Khai giảng khóa đàm thoại đặc biệt tại Top Globis
» Học tiếng nhật miễn phí tại Top Globis
» Học tiếng Nhật là niềm vui của bạn - Dạy tiếng Nhật là niềm tự hào của TOP GLOBIS.
» tranh cười
» clip cảm đọng quá mọi người ơi..
» 2 Different Tears (Korean ver) - WG :X
» Forever A1
» Nhị Thức NIUTON
» Ăn hành kí sự part 1
» Tell me goodbye_ BBang
» Hack map trong dota???